СОР № 1 Геометрия 8 класс Көпбұрыштар. Төртбұрыштарды зерттеу

Көпбұрыштар. Төртбұрыштарды зерттеу

Задание:

Сызбаның көмегімен параллелограммның периметрін табыңыз.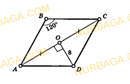

Решение:

ACD сызылған бұрышы 90°, сондықтан ол трапецияның үлкен негізі болып табылатын диаметрге сүйенеді.

 

AD=2R=16

 

Шеңберді төртбұрыштың айналасында сызуға болады, егер төртбұрыш үшін оның қарама-қарсы бұрыштарының мәндерінің қосындысы 180° болса. Демек, ABC бұрышына қарама-қарсы ADC бұрышы

 

∠ADC = 180° — ∠ABC = 180° — 120° = 60°

 

Гипотенузасы AD = 16 болатын ACD тікбұрышты үшбұрышында: ∠ ACD = 90° (берілген), ∠ADC = 60° (алынған), CD және ∠СAD табамыз,

 

CD = AD cos 60° = 16 0,5 = 8

 

және

 

∠CAD = 90° — ∠ADC = 90° — 60° = 30°

 

Трапеция тең қабырғалы

 

AB = CD — 8

 

BC табыңыз — трапецияның кіші табаны

 

Трапеция тең қабырғалы, сондықтан

 

∠BCD = ∠ABC = 120°

 

және

 

∠BAD = ∠ADC = 60°

 

ABC үшбұрышында

 

∠BCA = ∠BCD — ∠ACD = 120° — 90° = 30°

 

∠BAC = ∠BAD — ∠CAD = 60° — 30° = 30°

 

Демек, ΔABC тең қабырғалы

 

BC=AB=8