СОР № 1 Геометрия 8 класс Көпбұрыштар. Төртбұрыштарды зерттеу

Көпбұрыштар. Төртбұрыштарды зерттеу

Задание:

Сызбадағы төртбұрыштардың параллелограмм болатынын дәлелдеңіз.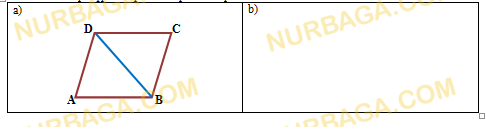

Решение:

Тіктөртбұрыштың критерийін дәлелдеңіз: егер параллелограммның диагональдары тең болса, онда бұл параллелограмм тіктөртбұрыш болады.

 

Дәлелдеу.

 

Суретте AC және BD диагональдары тең ABCD тіктөртбұрышы көрсетілген.

 

ABCD параллелограммының тіктөртбұрыш екенін дәлелдеп көрейік.

∆ABD және ∆ACD қарастырайық. Оларда AB \u003d CD, BD \u003d AC бар, AD жалпы жағы.

 

Демек, ΔABD және ΔΔACD үшбұрыштар теңдігінің үшінші белгісіне сәйкес тең.

 

Демек, ∠BAD = ∠CDA. Бұл бұрыштар AB және DC параллель түзулерімен және AD секантымен бір жақты. Демек, ∠BAD + ∠CDA = 180°. Сонда ∠BAD = ∠CDA =90°.

 

Сондықтан ABCD параллелограмы тіктөртбұрыш.