СОР № 1 Геометрия 8 класс Көпбұрыштар. Төртбұрыштарды зерттеу

Көпбұрыштар. Төртбұрыштарды зерттеу

Задание:

Суретте берілген трапецияның периметрін табыңыз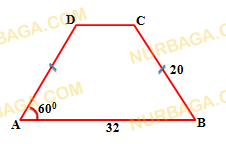

Решение:

Тең қабырғалы трапецияның төменгі табанындағы бұрыш 90°-тан аз, ал жоғарғы табанында 90°-тан үлкен, сондықтан ∠A = 60° табан бұрышы.

 

Біз қай жағы екенін білмейміз, тек олардың іргелес жатқанын білеміз. Сондықтан біз екі нұсқаны шешеміз.

 

1. AB – төменгі негіз.

 

H₁, H₂ ∈ AB; DH₁ , CH₂ ⊥AB ⇒ DH₁ ║ CH₂

 

ΔADH₁ = ΔCBH₂ — гипотенуза және сүйір бұрыш бойынша трапеция тәрізді тең қабырғалы.

 

AH₁ = H₂B — тең Δ сәйкес жақтары ретінде.

 

∠H₂CB = 90° — ∠CBH₂ = 90° — 60° = 30° — өткір төртбұрышты Δ.

 

H₂B \u003d BC / 2 \u003d 20/2 \u003d 10 — тікбұрышты Δ-де 30 ° бұрышқа қарама-қарсы жатқан аяқ ретінде.

 

H₁H₂ = 32 — 10*2 = 12 = себебі DH₁ ║ CH₂ және DH₁ = CH₂ — тең Δ сәйкес жақтары ретінде.

 

P — периметр.

 

P = AB + 2BC + CD = 32 + 40 + 12 = 84.

 

Жауабы: 84.

 

2. AB — жағы.

 

H₁, H₂ ∈ AD; BH₁ , CH₂ ⊥AD ⇒ BH₁ ║ CH₂ ⇒ BH₁ = CH₂ — параллель түзулер арасына салынған параллель кесінділер ретінде, сондықтан BCH₂H₁ – тіктөртбұрыш ⇒ H₁H₂ = BC =.

 

∆ABH₁ = ∆CDH₂ — гипотенуза және сүйір бұрыш бойынша трапеция тәрізді тең қабырғалы.

 

AH₁ = H₂D — тең Δ сәйкес жақтары ретінде.

 

∠ABH₁ = 90° — ∠BAH₁ = 90° — 60° = 30° — өткір төртбұрышты Δ.

 

AH₁ \u003d AB / 2 \u003d 32/2 \u003d 16 — тікбұрышты Δ түрінде 30 ° бұрышқа қарама-қарсы жатқан аяқ ретінде.

 

BC = AD BH₁ ║ CH₂ және BH₁ = CH₂ — тең Δ сәйкес жақтары ретінде.

 

AD = 20 + 16 2 = 52

 

P — периметр.

 

P = 2AB + BC + DA = 64 + 20 + 52 =.

 

Жауабы: 136.